RELACIONES GEOMÉTRICAS

 RELACIONES GEOMÉTRICAS

PROPORCIONALIDAD

Proporcionalidad es la relación que existe entre 2 figuras de igual forma y distinto tamaño.

Razón (K)

Dados 2 segmentos a y b, la razón es la relación entre las longitudes de ambos segmentos. Dados 4 segmentos (a, b, c y d) tomados dos a dos, se dice que son proporcionales si las razones son iguales: a/b=c/d. (Fig.1). Se denominan medios: b y c. Son extremos: a y d

Proporcionalidad directa:

Dos magnitudes son directamente proporcionales si varían de tal forma que su razón permanece constante. a/b=a’/b’=a”/b”=… = K

Proporcionalidad inversa:

Dos magnitudes son inversamente proporcionales si varían de tal forma que su producto permanece constante. a·b=a’·b’=a”·b”=… = K

TEOREMA DE TALES Y APLICACIONES

Si un haz de rectas paralelas cortan a 2 rectas concurrentes (Fig.2), los segmentos resultantes sobre la recta r son proporcionales a los determinados sobre la recta s. Son directamente proporcionales. AB/A’B’=BC/B’C’. También se cumple: AB/BC=A’B’/B’C’. Aplicaciones del Teorema de Tales:

División de un segmento en partes iguales

A partir de un extremo de un segmento, se traza una semirrecta sobre la que se marcan tantas divisiones iguales como partes en las que se quiera dividir el segmento. Unimos el último punto con el extremo del segmento y se trazan paralelas a esta recta por las divisiones obtenidas quedando así el segmento dividido en partes iguales (Fig.3).

División de un segmento en partes proporcionales

Se procede del mismo modo pero ahora las divisiones no son iguales. Las divisiones así obtenidas en el segmento mantendrán la misma proporción entre ellas que las dibujadas en la semirrecta trazada (Fig.4).

CUARTA PROPORCIONAL DE UN SEGMENTO Y APLICACIONES

Dados tres segmentos a, b y c, se denomina cuarta proporcional a un segmento d si éste cumple: a/b=c/d. Se trata de buscar un segmento ‘d’ que mantenga esta proporcionalidad.

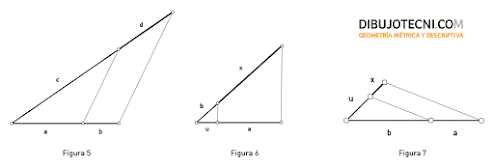
Trazamos 2 rectas r y s concurrentes en O.  Trasladamos los segmentos a y b sobre r a partir de O y c sobre s a partir de O. Unimos el extremo de ‘a’ con el extremo de ‘c’ y trazamos una paralela a esta recta por el extremo de ‘b’ obteniendo el extremo del segmento ‘d’ buscado y cuarta proporcional, pues se cumple que c/d mantiene la proporción a/b según el Teorema de Tales visto (Fig. 5).

Producto de 2 segmentos: a·b=c

Si se toma un segmento como unidad (u) y dados los segmentos a y b, se observa que: u/a=b/x; a/u=x/b; a·b=x·u; a·b=x. Por tanto, el segmento x es la cuarta proporcional de u, a y b, y el producto de a y b (Fig. 6).

Cociente de dos segmentos: a/b=x

Si se toma un segmento como unidad (u) y dados los segmentos a y b, se observa que: b/a=u/x; a/b=x/u; a/b=x. Por tanto, el segmento x es la cuarta proporcional de u, a y b, y el cociente de a y b (Fig. 7).

TERCERA PROPORCIONAL DE 2 SEGMENTOS Y APLICACIONES

Dados 2 segmentos a y b, es c tercera proporcional si se cumple que: a/b=b/c. Trazamos 2 semirrectas r y s con origen común llevando a y b a una de ellas desde el punto de intersección y b a la otra. Trazamos una paralela por el extremo b de la primera semirrecta a la unión de los otros dos extremos (Fig. 8).

Cuadrado de un segmento: b2=x

(Fig. 9) Dado b, tomamos como ‘a’ en la construcción un segmento de una unidad ‘u’ y se obserba que: u/b=b/x; b/u=x/b; b·b=x·u; b·b=x; x=b2

MEDIA PROPORCIONAL Y APLICACIONES

Dados los segmentos a y b, se denomina media proporcional al segmento c, si cumple: a/c=c/b. También se observa que: a·b=c2; c=√a·b

Podemos obtener la media proporcional mediante 2 procedimientos:

1. Teorema de la altura

Situamos los 2 segmentos dados uno a continuación del otro. Se traza una semicircunferencia de centro en M, punto medio de la suma de a y b (Fig. 10). Por el punto de contacto de los segmentos trazamos una perpendicular a estos que corta a la circunferencia y obtenemos la media proporcional buscada c.

2. Teorema del cateto

Dados los segmentos AB y AC (Fig. 11), los superponemos, trazamos el arco capaz de AC y le trazamos una perpendicular por B hasta cortar a la semicircunferencia. Desde la intersección obtenida unimos con A y obtenemos el segmento ‘x’, la media proporcional buscada. Aplicaciones de la media proporcional

Raíz cuadrada de un segmento ‘a’

Tomamos un segmento de una unidad de longitud ‘u’ y lo ponemos a continuación del segmento dado ‘a’ y obtenemos x como hemos expuesto en el teorema de la altura. √a=x; a=x2; a=x·x: a/x=x/u