SISTEMA DIÉDRICO
INTRODUCCIÓN
Forma parte de los llamados Sistemas de Representación Gráfica (Sistemas Axonométrico, Acotado, Cónico, etc…) estudiados en Geometría Descriptiva, esta tiene por objeto la representación en el plano de elementos o superficies tridimensionales distribuidos en el espacio.
Surge de la necesidad de sistematizar la estereometría (corte y mesura) de las piedras empleadas en las construcciones de la época y es en el siglo XVIII cuando Gaspar Monge, geómetra, físico y matemático francés (nacido en 1746 en Francia y considerado como el verdadero padre de la Geometría Descriptiva), sistematiza y hace gráficas las transformaciones y procesos estudiados hasta entonces por medios exclusivamente matemáticos, por lo que también se le denomina Sistema de Monge.
SIGNIFICADO
Se denomina Sistema por pertenecer a los Sistemas de Representación Gráfica (Diédrico, cónico, axonométrico…) .
Se denomina Diédrico, por utilizar, como sistema de referencia un ángulo Diédro o ángulo comprendido entre dos planos (di= dos, edro= plano), en este caso recto.
Se denomina Ortogonal por emplear proyecciones Cilíndricas Ortogonales para la representación de los diversos elementos distribuidos en el espacio.
ELEMENTOS DEL SISTEMA DIÉDRICO ORTOGONAL
Los planos de proyección (diedro ortogonal) y referencia se denominan en SDO, PLANO VERTICAL (PV) y PLANO HORIZONTAL (PH), en ellos se proyectan ortogonalmente las proyecciones verticales y horizontales respectivamente, de los elementos a representar.
La recta intersección de ambos planos se denomina LÍNEA DE TIERRA (LT).
Los espacios o regiones comprendidos entre los planos horizontal y vertical, se denominan DIEDROS, son cuatro en total, designándose como se indica en la ilustración. Además de estos elementos, principales, se utilizan con frecuencia otros como son:
PLANO DE PERFIL (PP), que es un plano perpendicular al vertical y horizontal, se utiliza cuando con las proyecciones horizontal y vertical no obtenemos suficientes datos del elemento representado y necesitamos por tanto otra proyección más, la de perfil en este plano.
PLANOS BISECTORES, son planos que dividen en dos ángulos iguales a los Diedros, son dos los bisectores. El espacio formado entre estos y los planos de proyección horizontal y vertical se denomina OCTANTE, son ocho los octantes, de ahí su nombre, se designan del 1º al 8º tal y como se indica en la ilustración de la figura 6.
SISTEMA DIÉDRICO. PUNTO: REPRESENTACIÓN, COORDENADAS Y ALFABETO DEL PUNTO.
Representación de un punto.
Un punto “A” se representa en este sistema mediante sus proyecciones ortogonales sobre el plano vertical y el horizontal. Estas proyecciones se denominan vertical y horizontal y se designan, con minúscula prima o mayúscula y subíndice 2 (a’ · A2) y minúscula o mayúscula y subíndice 1 (a · A1) respectivamente. Fig.7
Cuando trabajamos en Sistema Diédrico, hacemos coincidir el Plano Vertical de proyección del sistema de referencia con el papel del dibujo, representamos la línea de tierra quedando, de este modo, encima o debajo de ella las proyecciones efectuadas en este plano.
Lo proyectado sobre el Plano Horizontal queda sin embargo escorzado en la propia Línea de Tierra por lo que no es representativo. Para evitar esta situación abatimos dicho plano 90º en el sentido de las agujas del reloj, empleando como charnela o “bisagra” la propia Línea de Tierra, hasta hacerlo coincidir con el vertical de proyección. De este modo tenemos sobre el papel también las proyecciones horizontales de los elementos y ambos planos, Horizontal y Vertical, superpuestos sobre el papel del dibujo. Fig.8
El punto queda así representado por sus proyecciones horizontal y vertical entorno a la Línea de Tierra, sobre una perpendicular a esta trazada (en línea de puntos) y a unas distancias determinadas: la distancia de la proyección vertical a LT denominada COTA y la distancia de la proyección horizontal a LT denominada ALEJAMIENTO. Fig.9
La Cota es positiva cuando la proyección vertical del punto está por encima de LT, negativa si está por debajo y nula si está en ella.
El Alejamiento se considera positivo si la proyección horizontal está debajo de LT, negativo si está por encima y nulo cuando coincide con LT.
Coordenadas de un punto.
Un punto A, puede venir dado por sus COORDENADAS A (x, y, z), en donde “x” es la distancia sobre la línea de tierra desde la intersección de la perpendicular que contiene las proyecciones del punto con la propia línea de tierra hasta donde situemos el origen de coordenadas, “y” es el alejamiento y “z” la cota.
EJEMPLO: Para un origen de coordenadas situado en el extremo izquierdo de la línea de tierra, representamos el punto A (3, 2, 1).
El eje X es positivo del origen de coordenadas hacia la derecha y negativo en caso contrario. Fig.10
Alfabeto del punto.
Según la ubicación de un punto respecto del sistema de referencia establecido, así serán su cota y alejamiento y por tanto su representación en S.D.O. Un punto puede estar situado:
-En uno de los cuatro Diedros, (si está en el primero tendrá cota y alejamiento positivos, negativos ambos en el 3º, positiva la cota y negativo el alejamiento en el 2º y viceversa en el 4º.)
-Contenido en los Planos de Proyección, en cuyo caso tendrá nula la cota si está en el PH o el alejamiento si está en PV.
-Contenido en un plano bisector (tendrán igual magnitud su cota y su alejamiento, positivos ambos en el 1º diedro, negativos ambos en el 3º diedro y uno positivo y otro negativo en los diedros 2º y 4º).
-En la Línea de Tierra. En este caso son nulos los valores para la cota y el alejamiento.
RECTA. REPRESENTACIÓN, TRAZAS Y TIPOS DE RECTAS.
Representación de la recta en SDO
Sabemos que una recta es una sucesión de puntos y que dos puntos determinan una recta. En SDO una recta se representa mediante sus proyecciones sobre el Plano Vertical y el Plano Horizontal, denominadas Proyección Vertical y Proyección Horizontal de la recta respectivamente y designadas por minúscula prima y minúscula respectivamente (r’, r). Según algunos autores por minúscula con subíndices 2 y 1 respectivamente (r2, r1).
Para poder representar dichas proyecciones, bastará con representar las proyecciones de dos de los puntos de la recta y unir las proyecciones homólogas. Por ejemplo, para representar la recta R, representamos primero las proyecciones verticales y horizontales de A y B, puntos contenidos en ella. Uniendo -a’- con -b’- tendremos la proyección vertical de R, r’. Uniendo -a- con -b-, la proyección horizontal de “R”, r. Fig.12.
Pertenencia de un punto a una recta.
Un punto pertenece a una recta cuando las proyecciones vertical y horizontal del punto pertenecen a las proyecciones vertical y horizontal de la recta respectivamente.
Ejemplo.:
El punto C pertenece a R pues c’ y c pertenecen a r’ y r respectivamente. Los puntos D,E y F no pertenecen a R pues alguna de sus proyecciones o ambas no pertenecen a R. Fig.13.
El punto G no pertenece a R pues las proyecciones que coinciden con r’ y r no son las homólogas sino las contrarias, g está sobre r’ y g’ está sobre r, están invertidas y por tanto la pertenencia es solo aparente. Fig.14
Trazas de la recta
Se denominan Trazas de la recta a los puntos de intersección de esta con los planos de proyección horizontal, vertical y, en su caso, de perfil. Como cualquier otro punto, las trazas de la recta se representan por sus proyecciones horizontales y verticales.
Se denomina Traza Horizontal de una recta a la intersección de la recta con el plano horizontal de proyección, se designa con hache mayúscula, H y como cualquier otro punto, tiene proyección vertical (h’) y proyección horizontal (h), esta última coincidente con la verdadera traza. Fig.15.
Se denomina Traza Vertical de una recta a la intersección de la recta con el plano vertical de proyección, se designa con uve mayúscula, V y como cualquier otro punto tiene proyección vertical (v’) coincidente con la verdadera traza y proyección horizontal (v). Fig.15.
Tipos de rectas
Paralelas a alguno de los planos de proyección o a ambos:
Recta horizontal. La que es paralela al plano de proyección horizontal. Su proyección vertical es paralela a LT. Fig.17
Recta frontal. La que es paralela al plano de proyección vertical. Su proyección horizontal es paralela a LT. Fig.18
Perpendiculares a alguno de los planos de proyección:
Recta vertical. Perpendicular al plano horizontal de proyección. Su proyección vertical es perpendicular a LT. y su proyección horizontal queda representada por un punto. Fig.20
Recta de perfil. Presenta sus proyecciones normales a LT por pertenecer a un plano de perfil. Ver plano de perfil en este mismo tema. Fig 22.
Recta contenida en un bisector. Sus proyecciones forman un mismo ángulo con LT. En la figura 23 se representa una contenida en el primer bisector, primer diédro.
EL PLANO. REPRESENTACIÓN Y DESIGNACIÓN DE UN PLANO EN S.D.O. TRAZAS.
El plano se representa en S.D.O. por sus TRAZAS. Se denominan Trazas del plano a las rectas intersección de este con los planos vertical y horizontal de proyección.
La Traza Horizontal del plano es la recta intersección de este con el Plano Horizontal de proyección y la Traza Vertical es la intersección del plano con la el Plano Vertical de proyección. Si el plano es oblicuo, proyectante o de perfil, dichas trazas coinciden en un punto sobre la Línea de Tierra.
El plano en el espacio se designa con letra mayúscula, Q, con mayúscula prima la Traza Vertical, Q’ y mayúscula la Traza Horizontal, Q. Según algunos autores la designación correcta debe ser a1, a2 o cualquier otra letra griega acompañada de los subíndices 1 y 2 para las trazas horizontal y vertical respectivamente. Fig.25
DETERMINACIÓN DE UN PLANO.
Un plano puede venir dado directamente en sistema diédrico si nos aclaran la situación exacta de sus trazas. Frecuentemente tendremos que hallar las trazas de un plano que venga determinado de otro modo. Un plano puede venir determinado (cuatro casos).:
1. Determinación de un plano por dos rectas que se cortan, R y S.
Por una recta pueden pasar infinitos planos pero por dos rectas que se cortan solo pasa un plano. Fig. 28
Dadas las rectas R y S que se cortan en un punto A si queremos trazar un plano Q que contenga a R, debemos hacer pasar las trazas de este por las de la recta, son infinitos los planos que se pueden trazar que contengan a la recta.
Si queremos que, además de contener a R, el plano trazado Q contenga a S, haremos pasar las trazas de Q no solo por las de R sino también por las de S, de esta forma obtenemos el único plano determinado por R y S que se cortan. Fig. 29A y B.
2. Determinación de un plano por un punto y una recta, B y T.
Si trazamos desde el punto B una recta L que se corte con la dada T en un punto cualquiera P, estamos en la misma situación del ejercicio anterior, tenemos dos rectas L y T que se cortan, calculamos sus trazas y hacemos pasar por las homologas las trazas del plano buscado N. Fig.30.
3. Determinación de un plano por tres puntos no alineados, C, D y E.
Uniendo los puntos dos a dos (el C con el D y el E con el D, por ejemplo), mediante las rectas X y W, nos situamos de nuevo en el primer caso, siendo D en este caso el punto donde se cortan. Fig.31.
4. Determinación de un plano por dos rectas paralelas entre sí, M y Ñ.
Por dos rectas paralelas pasa un solo plano.
En SDO, dos rectas paralelas mantienen sus proyecciones homólogas también paralelas. Uniendo las trazas homólogas de estas tendremos definido el plano que determinan o en el que están contenidas, O. Fig.32.
TIPOS DE PLANOS.
En base a la posición de los planos dibujados respecto del sistema de referencia, se pueden tipificar los siguientes grupos y subgrupos:
1. Planos oblicuos a los planos de proyección
Los que no son paralelos ni perpendiculares a los planos de referencia del sistema. Presentan sus trazas oblicuas respecto de la línea de tierra. Fig.33.
2. Planos perpendiculares a los planos de proyección
Son perpendiculares a alguno de los planos de proyección o a ambos, se utilizan frecuentemente como planos auxiliares. Hay tres tipos:
Plano proyectante horizontal.
Es perpendicular al plano horizontal de proyección. Su traza vertical es perpendicular a la línea de tierra. Se denomina Proyectante Horizontal pues las proyecciones horizontales de todos los elementos contenidos en él coinciden en la traza horizontal de dicho plano. Fig.34
Plano proyectante vertical.
Es perpendicular al plano vertical de proyección. Su traza horizontal es perpendicular a la línea de tierra. Se denomina Proyectante Vertical pues las proyecciones verticales de todos los elementos contenidos en él coinciden en la traza vertical de dicho plano. Fig.35
Plano de perfil.
Son perpendiculares al plano vertical y horizontal de proyección. Sus trazas se presentan normales a la línea de tierra. Las proyecciones de los elementos en ellos contenidos, coinciden con sus trazas por lo que, y con objeto de obtener una proyección más representativa de sus elementos, abatimos este plano sobre el vertical de proyección presentándose de este modo en verdadera magnitud y forma. En la figura 40, abatimos un plano de perfil y apreciamos de este modo la ubicación de los puntos A y B en él contenidos. Fig.36
3. Planos paralelos a los planos de proyección.
Son paralelos a alguno de los planos de proyección, hay dos tipos:
Plano Horizontal.
Paralelo al horizontal de proyección. Su traza vertical es paralela a la línea de tierra y contiene las proyecciones verticales de los elementos contenidos en él. Por ser paralelo al plano horizontal no tiene traza horizontal. Fig. 37.
Plano Frontal.
Paralelo al vertical de proyección. Su traza horizontal es paralela a la línea de tierra y contiene las proyecciones horizontales de los elementos contenidos en él. Por ser paralelo al plano vertical no tiene traza vertical. Fig. 38.
4. Paralelos a la línea de tierra.
Presentan sus trazas vertical y horizontal paralelas a la línea de tierra. En la figura se traza un punto A perteneciente al plano, auxiliándonos de una recta R del plano. Fig. 39.
5. Planos que pasan por LT
Su intersección con los planos de referencia es la propia línea de tierra por lo que sus trazas no son representativas. Para representarlos se trazan las proyecciones de uno de sus puntos y se dibujan dos trazos por debajo de la línea de tierra, entorno a la recta de perfil que pasa por dicho punto. En la figura, se ha abatido la recta de perfil antedicha obteniéndose de este modo una idea clara de la ubicación relativa del plano. Obsérvese que esta recta es normal y corta a LT. Fig. 40.
6. Planos perpendiculares a los planos bisectores.
Plano perpendicular al primer bisector.
Calculamos la traza de perfil del plano bisector (coincidente con r”) y le trazamos una perpendicular en cualquiera de sus puntos (a”), quedando así determinada la traza de perfil Q” del plano buscado. Deshacemos el abatimiento del plano de perfil P y obtenemos Q y Q’. R es la recta intersección del bisector y el plano Q trazado, contiene al punto A equidistante a los planos de proyección y a X punto perteneciente a LT.
Son infinitos los planos normales al primer bisector, la única condición es que muestren sus trazas sobre un tercer plano de perfil, normales entre sí, las trazas vertical y horizontal del plano trazado, forman en cualquier caso idénticos ángulos con la línea de tierra. El trazado Q pasa además por X y A. Fig. 41. Un caso particular de plano normal a los bisectores es el plano de perfil, perpendicular a ambos bisectores y a los propios de proyección.
Plano perpendicular al segundo bisector.
Los ángulos que forman sus trazas con LT son idénticos pero en sentido contrario.
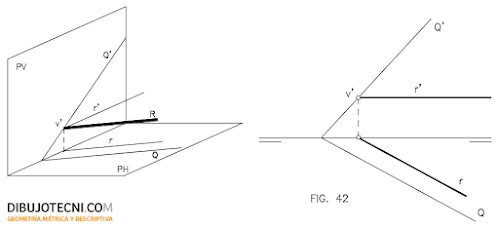
RECTAS PARTICULARES DEL PLANO.
Rectas horizontales del plano.
Son rectas horizontales y pertenecientes al plano. Fig 42
Son rectas frontales y pertenecientes al plano. Fig 43
Rectas de máxima pendiente e inclinación del plano.
Definen la dirección de máxima pendiente o inclinación de un plano, según se mida con el plano horizontal o vertical de proyección respectivamente.
Recta de máxima pendiente.
Es la dirección R por donde discurriría una gota de agua en un plano cualquiera Q, si hiciéramos coincidir el plano horizontal de proyección con el suelo. Será por tanto la recta del plano que forme mayor ángulo con el plano horizontal de proyección. En S.D.O. muestra esta recta R su proyección horizontal, r, perpendicular a la traza horizontal del plano. Naturalmente, esta recta está contenida en el plano Q, y por tanto sus trazas coincidentes con las homólogas de dicho plano. Fig.44
Es la dirección T por donde discurriría una gota de agua en un plano cualquiera P, si hiciéramos coincidir el plano vertical de proyección con el suelo. En S.D.O. muestra esta recta T su proyección vertical, t’, perpendicular a la traza vertical del plano. Naturalmente, esta recta está contenida en el plano P y por tanto sus trazas coincidentes con las homólogas de dicho plano. Fig. 45.
Rectas de perfil de un plano.
Las trazas de una recta de perfil R contenida en un plano Q coinciden con las trazas del plano, para conocer la ubicación de la recta con relación a los planos de referencia, abatimos en el plano vertical su proyección sobre un plano de perfil auxiliar P. Fig 46.
RESUMEN

































No hay comentarios:
Publicar un comentario