TEMA 3- TRIÁNGULOS
DEFINICIÓN Y DESIGNACIÓN.
Superficie plana limitada por tres rectas que se cortan dos a dos.
Los puntos de intersección de estas rectas se denominan vértices y se designan en mayúscula, los segmentos entre vértices lados y se designan en minúscula, igual al vértice opuesto.
Son polígonos convexos con sus diagonales coincidiendo con los lados.
PROPIEDADES FUNDAMENTALES.
Un lado es menor que la suma de los otros dos y mayor que su diferencia. b-c<a<b+c.
Si tiene dos lados iguales, sus ángulos opuestos también son iguales. Si a=b, a=b.
A mayor lado se opone siempre mayor ángulo.
La suma de los ángulos de cada vértice es siempre igual a 180º.
CLASIFICACIÓN DE LOS TRIÁNGULOS.
Según los lados
EQUILÁTERO. Si tiene sus tres lados iguales (a=b=c). Fig. 6.
ISÓSCELES. Si tiene dos lados iguales (c=b). Fig.7
ESCALENO. Ningún lado igual a otro. Fig.8
Según los ángulos.
ACUTÁNGULO. Los tres ángulos son agudos. Fig.9
RECTÁNGULO. Si tiene un ángulo recto. Fig.10
OBTUSÁNGULO. Si tiene un ángulo obtuso. Fig.11.
RECTAS NOTABLES Y CENTROS DEL TRIÁNGULO.
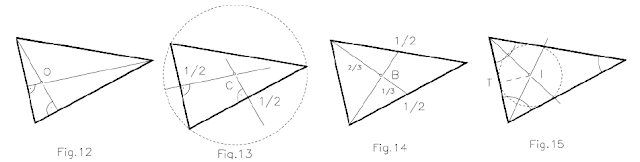
ORTOCENTRO. Punto donde se cortan sus alturas. Altura es la perpendicular de un vértice a su lado opuesto. Fig.12
CIRCUNCENTRO. Punto donde se cortan las mediatrices de los lados. Es centro de la circunferencia circunscrita del triángulo (contiene a sus vértices). Fig.13
BARICENTRO. Punto donde se cortan las medianas. Medianas son los segmentos que van de los vértices a los puntos medios de los lados opuestos. El baricentro es el centro de gravedad del triángulo y se encuentra respecto de los vértices a 2/3 de la mediana correspondiente. Fig.14
INCENTRO. Punto donde se cortan las bisectrices de los ángulos del triángulo. Es centro de la circunferencia inscrita en el triángulo (tangente a sus lados). Fig.15




No hay comentarios:
Publicar un comentario