VERDADERAS MAGNITUDES . ABATIMIENTO

 ABATIMIENTO

Habitualmente, las proyecciones en Sistema Diédrico Ortogonal de los planos, rectas y superficies representadas no muestran su forma real, las proyecciones sobre los planos de referencia generan deformaciones angulares y variaciones métricas cuando los elementos a representar están situados en planos oblicuos a los de proyección.

Para obtener la verdadera magnitud lineal y angular de un segmento, un ángulo o una superficie plana determinada colocaremos el plano que contiene a estos elementos o los elementos en sí, paralelos o contenidos en uno de los planos de proyección o viceversa, un plano de proyección paralelo a los elementos. De este modo las proyecciones se mostrarán en verdadera magnitud sobre el plano de proyección correspondiente pues, en proyecciones cilíndricas ortogonales, si las superficies a proyectar y el plano de proyección son paralelos o coincidentes no se producen deformaciones lineales ni angulares en la figura proyectada.

ABATIMIENTO DE LAS TRAZAS DE UN PLANO OBLICUO.

Abatiremos la traza vertical de un plano oblicuo Q sobre el plano horizontal de proyección. En realidad abatimos el plano en su totalidad pero es la traza vertical la que experimenta cambio gráficamente. La traza horizontal será la charnela del abatimiento permaneciendo por tanto invariable. Podemos trabajar de dos modos distintos:

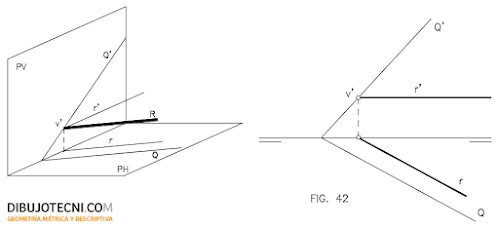
Tomamos un punto A de la traza Q’ y lo abatimos sobre el plano horizontal en A1, uniéndolo con N, punto de concurrencia de las trazas sobre la línea de tierra, obtendremos la traza Q’1 abatida. Para abatir el punto A, trazamos por él una recta R de máxima pendiente del plano, esta recta corta a la traza horizontal del plano en el punto m.

Las proyecciones del punto a’ y a, forman junto a m, un triángulo rectángulo cuya hipotenusa, el segmento a’m, es la recta de máxima pendiente del plano y debe de coincidir tras el abatimiento, por ser una recta del plano Q, con el plano horizontal de proyección. La recta de máxima pendiente es pues radio de un arco de circunferencia de centro m que tendremos que trazar hasta ubicarla sobre el plano horizontal de proyección y localizar así en su extremo la posición de A abatido.

Para poder trazar esta circunferencia representada en la figura 6 en visión espacial, en proyecciones diédricas, abatimos previamente el mencionado triángulo sobre el plano horizontal de proyección tomando como charnela su cateto am. Para ello trazamos una recta paralela a la traza horizontal de Q o normal al propio cateto am por a, llevando sobre ella y a partir de a, la magnitud del cateto aa’ que no es sino la cota del punto A conocida, obtenemos de este modo el punto a’0, vértice del triángulo abatido. Uniendo a’0 con m, invariable en este abatimiento previo, obtenemos la hipotenusa que no es sino la recta R abatida sobre plano horizontal de proyección y radio del arco que tenemos que trazar.

Situado el triángulo sobre el plano horizontal de proyección podemos trazar ya el arco de centro m y radio m-a’0 hasta cortar a la prolongación del cateto am en A1 punto buscado. Uniendo el punto n, vértice de las trazas del plano Q en la línea de tierra con A1, obtenemos la traza vertical del plano Q abatida sobre el plano horizontal de proyección en Q’1. Fig. 7.

En cualquier abatimiento, todos los puntos del plano abatido describen circunferencias situadas en planos normales al plano a abatir. Estas circunferencia tienen su centro en la charnela y radios que van desde el punto de intersección entre la circunferencia y la charnela a los respectivos puntos. Si los puntos están situados en una de las trazas (la contraria a la charnela escogida), los radios mencionados serán rectas de máxima pendiente o inclinación según abatamos sobre el plano horizontal o vertical de proyección respectivamente.

ABATIMIENTO DE UN PUNTO SITUADO EN UN PLANO DADO Q.

Cuando hablamos de abatir un punto, nos referimos a abatir el plano que lo contiene para poder de este modo ver la situación del punto en alguno de los planos de proyección, en este caso sobre el plano horizontal. Primero comprobaremos mediante una recta del plano, en este caso la horizontal T, que el punto pertenece efectivamente al plano Q.

 Hacemos pasar por el punto dado A, una recta de máxima pendiente R y a partir de la proyección horizontal del punto, trazamos un segmento paralelo a la traza horizontal del plano cuya magnitud sea igual a la COTA del punto A, uniendo el extremo de este segmento, a’o, con el punto m de intersección entre la proyección horizontal de R y la traza Q del plano, obtenemos la hipotenusa del triángulo rectángulo radio del giro según vimos en el ejercicio anterior, primer método. Haciendo centro en m y con radio igual a la trazamos un arco hasta cortar a la prolongación de la proyección horizontal de R obteniendo así la ubicación sobre el plano horizontal del punto A abatido, A1. Fig.10

En la figura 11, hemos abatido el punto A sobre el plano horizontal de proyección auxiliándonos de la traza vertical del plano abatida en Q’1 según el segundo método del ejercicio anterior. Para ello hemos abatido un punto de la traza vertical, v’ en v’1 que unido con n define Q’1. Trazamos una recta perpendicular por la proyección horizontal de A a Q y una recta paralela a t por v’1 (recta horizontal T abatida en T1), donde ambas se cortan tenemos A1.

El abatimiento de un punto sobre el plano vertical de proyección se realiza del mismo modo pero a partir de una recta de máxima inclinación en el primer caso y auxiliándonos de la traza horizontal del plano dado, abatida sobre el plano vertical de proyección.

ABATIMIENTO DE UN SEGMENTO SITUADO EN UN PLANO DADO.

Para abatir un segmento dado AB, situado en un plano Q, comprobaremos primero que efectivamente pertenece al plano mediante, por ejemplo, rectas horizontales del plano Q, T y S que pasen por los extremos del segmento A y B respectivamente.

Abatiremos los puntos A en A1 y B en B1, sobre el plano horizontal en este caso, como hemos visto en las figuras 10 y 11, uniendo A1 con B1 tendremos abatido sobre el plano horizontal de proyección el segmento dado y por tanto en verdadera magnitud.. En la figura 12 se realiza el ejercicio a partir de una recta de máxima pendiente del plano que pase por A y en la figura 13 a partir de la traza vertical Q’ del plano abatida.

ABATIMIENTO DE UNA SUPERFICIE PLANA SITUADA EN UN PLANO DADO.

Como en el caso del segmento resuelto anteriormente, lo primero es comprobar si realmente pertenece dicha superficie al plano. Para ello emplearemos rectas auxiliares, por ejemplo, horizontales.

La superficie a abatir será en el ejemplo un triángulo obtusángulo de vértices A, B y C. El procedimiento a seguir es exactamente el mismo que el empleado en el abatimiento de un punto o de un segmento vistos anteriormente. En el ejercicio de la figura 14 el abatimiento se efectúa sobre el plano horizontal de proyección y se resuelve el problema por el segundo método estudiado, es decir, auxiliándonos de la traza del plano que contiene a la superficie plana abatida sobre el plano horizontal de proyección.

Podemos simplificar el trazado haciendo uso de la relación de afinidad existente entre una de las proyecciones de la figura y la propia figura abatida como veremos en el ejercicio siguiente.

ABATIMIENTO DE UNA SUPERFICIE PLANA, SIMPLIPLIFICANDO MEDIANTE AFINIDAD.

Una afinidad queda determinada como sabemos si conocemos el eje de afinidad, la dirección y la relación de afinidad o un punto afín de la figura dada.

La relación de afinidad entre las proyecciones diédricas de una figura y la figura abatida sobre uno de su plano de proyección correspondiente tiene como eje de afinidad la charnela de abatimiento y dirección de afinidad normal a la charnela, solo necesitamos conocer un punto afín de una de las proyecciones de la figura que no es sino un punto abatido por cualquiera de los métodos estudiados.

En el ejercicio de la figura 15, abatimos el punto A en A1 y resolvemos B1 y C1 por afinidad siendo n y ñ puntos dobles de esta relación. Podemos observar que el trazado del ejercicio se simplifica notablemente.

DESABATIMIENTO DE UNA SUPERFICIE PLANA SOBRE UN PLANO DADO Q.

Se puede dar el caso en que necesitemos situar un punto, segmento o superficie ubicados en uno de los planos de proyección, sobre un plano dado Q, tendremos pues que desabatir estos elementos invirtiendo los pasos estudiados en los abatimientos.

En el ejemplo de la figura 16, conocida la figura A1, B1 C1 abatida sobre el plano horizontal de proyección y dado el plano Q, desabatiremos el triángulo. Podemos desabatir uno de sus vértices y calcular el resto mediante la afinidad existente entre la superficie abatida y la proyección horizontal de la figura contenida en el plano oblicuo Q.

Para desabatir uno de los tres vértices, en el ejemplo el vértice A1, y dejar de este modo definida la relación de afinidad, operamos de modo inverso al abatimiento de un punto, para ello abatimos previamente la traza vertical del plano sobre el plano horizontal de proyección y obtenemos Q’1, trazamos por  A1 una recta normal y otra paralela a la traza horizontal del plano y obtenemos en la intersección de esta última con Q’1 el punto m1. Por m1 trazamos una recta normal a la traza Q hasta cortar a la línea de tierra en m desde donde trazamos otra recta paralela a Q hasta cortar a la normal trazada por A1 a Q, obtenemos de este modo la proyección horizontal del punto A, a.

En esta operación nos hemos auxiliado de una recta horizontal del plano que contiene a A1 y la hemos desabatido para obtener la proyección horizontal de A. Obtenido a, y establecida por tanto la afinidad, trazamos las proyecciones horizontales de B y C. Para calcular las proyecciones verticales de la figura contenida en el plano dado Q, nos auxiliamos de rectas horizontales del plano Q que contengan a las proyecciones a, b y c. Obtendremos de este modo los puntos a’, b’ y c’.

VERDADERAS MAGNITUDES .DISTANCIAS EN EL SISTEMA DIÉDRICO

 

 DISTANCIAS

SISTEMA DIÉDRICO. DISTANCIAS.

Los problemas de distancias entre rectas, planos, rectas y planos, puntos y rectas etc., se reducen siempre a calcular la distancia entre dos puntos.

La verdadera distancia entre dos puntos no viene, en sistema diédrico ortogonal, reflejada en sus proyecciones salvo que el segmento que estos dos puntos definen sea paralelo o se encuentre contenido en uno de los planos de proyección.

Para poder apreciar en verdadera magnitud lineal la distancias entre dos puntos, colocaremos pues el segmento que entre los dos definen paralelo a uno de los planos de proyección, contenido en él o viceversa, colocamos uno de los planos de proyección paralelo al segmento en cuestión, utilizando para ello métodos como abatimientos, cambios de plano o giros.

DISTANCIA ENTRE DOS PUNTOS

Vamos a resolver este ejercicio por 4 métodos distintos.

Dados dos puntos A y B por sus proyecciones diédricas, situaremos en los dos primeros métodos una de las proyecciones del segmento que definen paralela a uno de los planos de proyección convirtiéndolo en frontal u horizontal para apreciar la distancia entre A y B en verdadera magnitud.

1er método: mediante giro

Convertimos el segmento AB en, por ejemplo, recta frontal, es decir paralelo al plano vertical, tomando como eje de giro una recta vertical que pasa en el ejemplo de la figura 17 por el extremo B del segmento. La nueva proyección vertical del segmento determina la verdadera magnitud del mismo y por tanto la distancia real existente entre los puntos A y B.

2º método: mediante cambio de plano

Convertimos el segmento AB en una recta horizontal en el ejemplo de la figura 18 mediante cambio de plano horizontal. La nueva proyección horizontal del segmento se apreciará en verdadera magnitud.

3er método: mediante abatimiento

Calculamos las trazas de un plano Q que contenga a la recta definida por los punto A y B dados y abatimos el segmento sobre uno de los planos de proyección, en el ejemplo de la figura 19 abatimos sobre el plano horizontal de proyección a partir de la traza horizontal del plano. El segmento AB abatido está en verdadera magnitud.

4º método: simplificando el abatimiento

En la figura 20 podemos apreciar que la distancia entre los puntos A y B es la hipotenusa de un triángulo rectángulo en donde los catetos, conocidos, son uno la proyección horizontal del segmento AB y el otro la diferencia de cotas entre los puntos A y B. En realidad se está abatiendo el triángulo rectángulo abB sobre un plano paralelo al plano horizontal de proyección, tomando como charnela el cateto ab. Esta misma operación podemos realizarla tomando como catetos la proyección vertical del segmento a’b’ y la diferencia de alejamientos entre los puntos A y B.

DISTANCIA DE UN PUNTO A UN PLANO

La distancia de un punto A a un plano P es un segmento (el segmento AE en el ejemplo), siendo E el punto de intersección entre el plano P y una recta perpendicular a él trazada por el punto dado A. 

En proyecciones diédricas, trazamos directamente por A una recta R normal al plano dado P.

Para calcular el punto de intersección E entre la recta trazada R y el plano P nos auxiliamos de un plano que contenga a la recta, en el ejemplo de la figura 21 hemos tomado el plano Q proyectante vertical, la distancia entre los puntos A y E es la distancia buscada.

Para apreciarla en verdadera magnitud operamos según alguno de los cuatro métodos descritos en el ejercicio anterior. En el ejemplo se ha calculado la verdadera magnitud girando el segmento AE hasta convertirlo en frontal.

DISTANCIA DE UN PUNTO A UNA RECTA.

La distancia de un punto A a una recta R es un segmento AE siendo E el punto de intersección de una recta D perpendicular a R y trazada desde A.

En proyecciones diédricas, la perpendicularidad entre rectas no se conserva por lo que no podemos trazar directamente por A la recta D mencionada.

Para resolver este ejercicio, trazaremos por A un plano P normal a la recta R. Conteniendo a la recta R trazaremos

un plano Q que genera con el plano P la recta T de intersección entre ambos. El punto de intersección E entre las rectas R y T será el extremo del segmento AE buscado. Fig. 22. A continuación detallo esta construcción en proyecciones diédricas.

Como ha quedado visto, para localizar el segmento AE, tendremos que auxiliarnos de un plano P perpendicular a R, este lo trazaremos auxiliándonos a su vez de una recta S horizontal que, conteniendo al punto A presente su proyección horizontal normal a la proyección horizontal de R. (Véase rectas perpendiculares entre sí). Conteniendo a la recta S y por tanto al punto A, trazamos el plano P perpendicular a la recta R.

El plano P trazado corta a la recta R en el punto E, extremo buscado del segmento. Para localizar dicho punto (intersección recta-plano), trazamos un plano auxiliar Q proyectante vertical en el ejemplo, que contenga a la recta R, la intersección de los planos P y Q genera la recta T y esta se corta con la recta R en el punto E.

El segmento AE, perteneciente a la recta D, nos proporciona en verdadera magnitud la distancia buscada entre el punto A y la recta R.

La verdadera magnitud del segmento se ha calculado por giro. Fig. 23

DISTANCIA ENTRE DOS RECTAS PARALELAS

La distancia entre dos rectas paralelas R y S viene definida por un segmento AE perpendicular a ambas.

Al no poder trazar directamente en Sistema Diédrico Ortogonal rectas perpendiculares entre sí, tendremos que trabajar del siguiente modo:

Trazamos un plano P perpendicular a ambas rectas y calculamos los puntos de intersección A y E de este con las rectas R y S. Calculamos la verdadera magnitud del segmento AE.

Para calcular la intersección de las rectas R y S con el plano P, nos auxiliaremos de planos proyectantes O y Q que contengan a R y S respectivamente, estos generarán con el plano P las rectas de intersección T y K respectivamente. Los puntos de intersección de las rectas T con R y K con S son los puntos A y E buscados.

La verdadera magnitud del segmento AE no se resuelve en el ejemplo de la figura 24 para no restar claridad al dibujo.

DISTANCIA ENTRE DOS PLANOS PARALELOS

Para calcular la distancia existente entre dos planos P y Q paralelos, bastará con trazar una recta R perpendicular a ambos.

El segmento AE definido por los puntos de intersección de la recta R con los planos P y Q determinará la distancia buscada. En proyecciones diédricas, trazaremos la recta R directamente perpendicular a P y Q.

Para calcular los puntos A y E (intersección recta-plano), trazaremos por R un plano O auxiliar (en el ejercicio de la figura 25, proyectante vertical) que contenga a la recta R, este genera en los planos P y Q las rectas intersección T y K. Los puntos de corte de estas rectas con R y S son los puntos A y E buscados. La verdadera magnitud del segmento AE se resuelve por cualquiera de los métodos estudiados.

MÍNIMA DISTANCIA ENTRE DOS RECTAS QUE SE CRUZAN

Para calcular la mínima distancia existente entre dos rectas que se cruzan K y R, trazamos por cualquier punto de una de las dos rectas una recta paralela a la otra recta dada (en el ejemplo del ejercicio 26 por el punto A de la recta R trazamos una recta T paralela a K).

Obtenemos de este modo dos rectas que se cortan y que por tanto definen un plano, el plano P.

Podremos obtener la distancia entre las rectas K y R sin más que trazar desde cualquier punto de la recta K (en el ejemplo el punto O) una recta S perpendicular al plano P, el segmento OE determina dicha distancia siendo E el punto de intersección entre la recta S y el plano P. Queda de este modo el ejercicio reducido a calcular la distancia de un punto a un plano ya estudiado en este tema.

PARALELISMO Y PERPENDICULARIDAD

 PARALELISMO Y PERPENDICULARIDAD

 1. DEFINICIÓN DE PARALELISMO

Se dice que dos elementos son paralelos cuando mantienen una distancia constante entre sí. Esto significa que nunca se cortarán y, por tanto, no contienen ningún punto en común.

Esto es aplicable a los tres casos que veremos de paralelismo entre rectas, entre planos y entre recta y plano.

Paralelismo Sistema Diédrico

2. PARALELISMO ENTRE RECTAS

Dos rectas son paralelas entre sí cuando sus proyecciones son paralelas.

Es muy importante observar que las proyecciones verticales tienen que ser paralelas entre sí y las proyecciones horizontales paralelas entre sí. De tal modo que si tenemos dos rectas dadas por sus proyecciones r’-r, s’-s, para que sean paralelas, r’ deberá ser paralela a s’ y r deberá ser paralela a s.

De esta manera, si tienes que dibujar una recta u´-u paralela a una dada t´-t por un punto a’-a, simplemente tendrás dibujar la proyección horizontal u paralela a t pasando por a y la proyección vertical u’ paralela a t’ pasando por a’.

01-Rectas paralelas

EXCEPCIÓN

Rectas de perfil: Las proyecciones de una recta de perfil son siempre perpendiculares a la Línea de Tierra, pero eso no significa que todas las rectas de perfil sean paralelas entre sí. Necesitaremos hacer una tercera vista de perfil para ver la dirección de las rectas y comprobar si son o no paralelas.

02-Rectas paralelas excepción.

3. PARALELISMO ENTRE RECTAS Y PLANOS

Una recta es paralela a un plano cuando es paralela a una recta contenida en el plano.

Esto significa que el paralelismo entre rectas y planos no se ve directamente en diédrico. Necesitaremos siempre una recta auxiliar para comprobar que son paralelos.

Por ejemplo, para dibujar una recta t´-t paralela a un plano dado Q´-Q que pase por un punto a’-a tendremos que dibujar una recta s’-s cualquiera contenida en el plano Q’-Q y luego trazar por el punto una recta paralela a dicha recta s’-s. (recuerda que para dibujar una recta contenida en un plano es necesario que sus puntos traza estén contenidos en las trazas del plano)

03-Plano paralelo a recta

Para dejar aún más claro este apartado, que es fundamental, te voy a poner dos ejercicios más que son comunes.

1. Te pueden pedir que compruebes si una recta r’-r es paralela a un plano P’-P. Para ello, deberás dibujar una recta s´-s paralela a la dada que pase por un punto a’-a del plano y deberás comprobar si esta recta está contenida en el plano. Si lo está, la recta R y el plano P son paralelos.

04-Plano paralelo a recta

2. También te pueden pedir que dibujes un plano Q´-Q paralelo a una recta t’-t que pase por un punto exterior b’-b. Para ello tendrás que dibujar una recta u´-u paralela a la recta dada, obtener sus puntos traza y por ellos trazar un plano cualquiera Q’-Q. Puedes estar seguro de que la recta T y el plano Q son paralelos.

05-Plano paralelo a recta

4. PARALELISMO ENTRE PLANOS

Dos planos son paralelos entre sí cuando sus trazas son paralelas.

El paralelismo entre planos se ve directamente en Sistema Diédrico. Obviamente las trazas verticales tienen que ser paralelas entre sí y las trazas horizontales, paralelas entre sí. Dados dos planos en Sistema Diédrico definidos por sus trazas P’-P, Q’-Q, estos serán paralelos cuando P’ sea paralelo a Q’ y a su vez P sea paralelo a Q.

Para trazar un plano W’-W paralelo a uno dado X’-X pasando por un punto a’-a necesitaremos utilizar una recta auxiliar r’-r paralela al plano dado para definir los puntos traza por los que pasarán las trazas del plano paralelo. En este caso, te recomiendo que utilices la recta que más cómoda te resulte (horizontal, frontal…)

06-Planos paralelos

EXCEPCIONES

Planos paralelos a la Línea de Tierra

Planos que contienen a la Línea de Tierra

Estos dos tipos de planos tienen trazas paralelas a la Línea de Tierra o coinciden con ella, pero eso no significa que siempre sean paralelos entre sí. Para comprobar el paralelismo entre estos planos será necesario recurrir a la vista de perfil, que nos indicará la verdadera magnitud de su inclinación.

En el plano de perfil podremos definir si este tipo de planos son paralelos entre sí.

07-Planos paralelos

PERPENDICULARIDAD

1. RECTA PERPENDICULAR A PLANO

Una recta es perpendicular a un plano cuando sus proyecciones son perpendiculares a las trazas del plano.

Para dibujar una recta perpendicular a un plano dado por un punto, simplemente tendremos que dibujar sus proyecciones perpendiculares a las trazas del plano pasando por el punto.

01 Recta perpendicular a plano

Excepción: Planos paralelos a la Línea de Tierra y planos que contienen a la Línea de Tierra. En ambos casos, la recta perpendicular es una Recta de Perfil. Para ver la perpendicularidad necesitaremos un plano auxiliar de perfil.

02 Recta perpendicular a plano

2. RECTAS PERPENDICULARES ENTRE SÍ

Dos rectas perpendiculares en el espacio, en general, no tienen sus proyecciones perpendiculares. Únicamente cuando una de las rectas es paralela a uno de los planos de proyección, las proyecciones de ambas rectas sobre este plano serán perpendiculares.

Esto quiere decir que, para dos rectas perpendiculares en el espacio:

Si una es horizontal, sus proyecciones horizontales son perpendiculares

Si una es frontal, sus proyecciones verticales son perpendiculares

03 Recta perpendicular a recta

Una recta es perpendicular a otra cuando está contenida en un plano perpendicular a dicha recta. Una recta es perpendicular a un plano cuando sus proyecciones son perpendiculares a las trazas del plano.

De aquí se deduce que un plano perpendicular a la recta contiene las infinitas rectas perpendiculares a dicha recta.

04 Recta perpendicular a recta

RECTA PERPENDICULAR A OTRA POR UN PUNTO

Para dibujar una recta perpendicular a otra dada por un punto existen 2 posibilidades:

Dibujar una recta horizontal o frontal que tenga sus proyecciones horizontales o verticales respectivamente perpendiculares a la dada y que pase por el punto.

Dibujar un plano perpendicular a la recta dada que pase por el punto y en él contener una recta. Esto lo veremos en el siguiente apartado.

3. PLANO PERPENDICULAR A RECTA

Un plano es perpendicular a una recta cuando sus trazas son perpendiculares a las proyecciones de la recta (igual que hemos visto en el apartado 1)

Excepción: Rectas de Perfil. Para dibujar un plano perpendicular a una recta de perfil tendremos que utilizar un plano auxiliar de perfil.

05 Plano perpendicular a recta

PLANO PERPENDICULAR A RECTA POR UN PUNTO

Para dibujar un plano perpendicular a una recta por un punto dado utilizaremos una recta auxiliar que sea perpendicular a la dada y pase por el punto. Por sus puntos traza dibujaremos el plano perpendicular.

Ejemplo: Dibujar el plano P’-P perpendicular a la recta dada r’-r y que pase por el punto a’-a.

Dibuja la proyección horizontal de la recta s’-s que pase por a y sea perpendicular a la proyección horizontal r de la recta.

Dibuja proyección vertical s’ de la recta, que pase por a’ y sea paralela a la Línea de Tierra.

Obtén el punto traza vertical de dicha recta s’-s.

Pasa la traza vertical P’ del plano perpendicular a la proyección vertical r’ de la recta

Por el punto de corte de P’ con la Línea de Tierra dibuja la traza horizontal P del plano perpendicular a la proyección horizontal r de la recta.

06 Plano perpendicular a recta

4. PLANOS PERPENDICULARES ENTRE SÍ

Dos planos son perpendiculares entre sí cuando uno de ellos contiene una recta perpendicular al otro.

Se deduce de aquí que:

Sus trazas no tienen que ser necesariamente perpendiculares.

Dado un plano, los infinitos planos que contienen a una recta perpendicular al dado serán perpendiculares a este.

PLANO PERPENDICULAR A OTRO POR UN PUNTO

Dado un plano P’-P y un punto a’-a, dibujar otro plano Q’-Q perpendicular al dado.

Dibuja una recta r’-r perpendicular a P’-P que pase por a’-a y halla sus puntos traza.

Dibuja cualquier plano que contenga a la recta r’-r, es decir, cuyas trazas pasen por los puntos traza de la recta.

Como puedes comprobar, este ejercicio tiene infinitas soluciones.

07 Plano perpendicular a plano

PLANO PERPENDICULAR A OTROS DOS POR UN PUNTO

Dados los planos P’-P y Q’-Q y un punto a’-a, dibujar otro plano J’-J perpendicular a los 2 dados.

Dibuja una recta r’-r perpendicular a P’-P que pase por a’-a y halla sus puntos traza.

Dibuja una recta s’-s perpendicular a Q’-Q que pase por a’-a y halla sus puntos traza (basta con encontrar 3 puntos traza de ambas rectas)

Dibuja el plano que contiene ambas rectas r’-r y s’-s, es decir, cuyas trazas pasan por los puntos traza de ambas rectas.

Este ejercicio tiene una única solución.

SISTEMA DÍÉDRICO INTERSECCIONES

SISTEMA DIÉDRICO INTERSECCIONES 

 TIPOS DE INTERSECCIONES

PLANO -PLANO= RECTA

                                   

RECTA -RECTA = PUNTO

PLANO -RECTA = UN PUNTO

INTERSECCIÓN DE PLANOS.

La intersección de dos planos P y Q, genera una recta I. El método general para calcular la intersección entre dos planos P y Q consiste en calcular las rectas intersección R, S, T y F de estos con otros dos auxiliares W y X de fácil trazado. Unimos seguidamente los puntos de intersección A y B de las rectas intersección pertenecientes a un mismo plano auxiliar y obtenemos de este modo la recta intersección I buscada. Fig. 47

Intersección de dos planos oblicuos.

Dados dos planos oblicuos P y Q, aplicaremos el método general comentado siendo en este caso los planos auxiliares a tomar X y W los de proyección vertical y horizontal y las rectas intersección de los auxiliares con los planos dados sus trazas correspondientes.

Así pues, la intersección de las trazas homónimas o correspondientes al plano vertical y la intersección de las trazas horizontales de ambos planos determinarán los puntos A y B anteriormente mencionados y que unidos definen como sabemos a la recta intersección I entre P y Q buscada.

Obsérvese que además, A y B se corresponden con las trazas vertical v’ y horizontal h de la recta en cuestión. Fig. 48

Intersección de plano oblicuo p con plano horizontal Q.

La recta intersección resultante a de pertenecer al plano horizontal Q dado luego será horizontal. También a de pertenecer al plano oblicuo P por lo que será una horizontal de P. Como sabemos, los planos y las rectas horizontales no presentan traza horizontal pues son paralelos al plano horizontal de proyección.

Empleamos el mismo método que en el ejercicio anterior y obtenemos la traza vertical v’ de la recta solución en la intersección de P’ y Q’, no podemos sin embargo operar de igual modo para calcular la traza horizontal de la recta horizontal solución pues Q no presenta traza horizontal pero sabemos que la recta horizontal, por pertenecer a P tiene que ser paralela a la traza horizontal de éste. Trazamos por tanto una recta horizontal de P que pase por v’. La proyección vertical de I, i’ coincidirá con la traza vertical de Q, Q’ pues éste es proyectante vertical. Fig. 49.

Intersección de plano oblicuo P, con plano frontal Q.

Este caso es idéntico al anterior, está resuelto en la Figura 50.

Intersección de un plano oblicuo P con un plano proyectante vertical Q.

El trazado es idéntico al empleado para calcular la intersección entre dos planos oblicuos. Observaremos que la proyección vertical de I, i’, coincide con la traza vertical de Q por ser éste un plano proyectante vertical. Fig. 51

Esta intersección es similar a la anterior, resultando coincidentes en proyección diédrica la proyección horizontal i y la traza horizontal de Q, por ser este plano proyectante horizontal. Fig.52.

                         

Intersección de plano oblicuo con plano proyectante horizontal e intersección de proyectante horizontal y vertical entre sí.

Intersección de planos proyectantes entre sí.

Intersección de planos proyectantes horizontal y vertical.

Se emplea el método general estudiado. Donde se cortan las trazas homólogas de los planos, tenemos las trazas de la recta intersección. Las proyecciones de la recta son coincidentes en este caso con las trazas de los planos por ser éstos proyectantes. Fig.53

Intersección de proyectantes verticales entre sí.

La traza vertical de la recta v’ está en la intersección de las trazas verticales de los planos. La recta resultante será de punta siendo su proyección horizontal i perpendicular a la línea de tierra. La proyección vertical i’ coincide con v’. Fig. 54

Intersección de proyectantes horizontales entre sí.

Este caso es similar al anterior. La proyección vertical de la recta será perpendicular ahora a la línea de tierra por ser I una recta vertical y su proyección horizontal será un punto coincidente con la traza horizontal h por esta misma razón. Fig.55

Intersección de un plano oblicuo con uno paralelo a LT.

Se procede según el método habitual y obtenemos v’ y h, trazas de la recta buscada. Fig.56

Intersección de proyectantes horizontales entre sí. Intersección de plano oblicuo con paralelo a la línea de tierra.

Intersección de proyectantes horizontales entre sí. Intersección de plano oblicuo con paralelo a la línea de tierra.

Intersección de planos paralelos a LT.

La intersección resultante será una recta paralela a la línea de tierra. No se puede proceder del modo habitual pues las trazas homónimas de los planos son paralelas entre sí. Podemos resolver este ejercicio por dos métodos:

1. Auxiliándonos con un plano oblicuo.

Si trazamos un tercer plano oblicuo O y calculamos su intersección con los planos P y Q dados, obtenemos dos rectas intersección r y s una con cada plano, estas se cortarán en X punto por el que pasa la recta I que como sabemos a de ser paralela a LT. Fig. 57

                         

2. Mediante un plano de perfil.

Trazamos un plano de perfil O y abatimos las trazas con este Q” y P” sobre el plano vertical, ambas se cortarán en el punto X representado por su tercera proyección x” y que estará contenido en la recta solución. Obtenemos las proyecciones x y x’ del punto X y pasamos por ellas las proyecciones i’ y i de la recta solución, paralelas a LT. Fig. 58

Intersección de un plano con los planos bisectores.

Por tener los planos bisectores sus trazas confundidas con LT, no podemos proceder según el método habitual. Sabemos que todos los puntos pertenecientes a un bisector equidistan de los planos de proyección, es decir, tienen igual cota que alejamiento.

Para resolver este problema dibujaremos las proyecciones de un punto A perteneciente al plano bisector Q, primer bisector en el ejemplo y al propio plano P dado auxiliándonos de una recta del plano, en el ejemplo horizontal. A es un punto de la recta intersección solución pues pertenece a ambos planos (pertenece a P por estar situado en una recta horizontal del plano P y al bisector por tener igual cota que alejamiento), calculamos otro punto B por el mismo procedimiento quedando determinada la recta. Para mayor simplicidad, el punto B tomado es el de concurrencia sobre la línea de tierra de las trazas del plano P. B pertenece a P y al bisector. Fig. 59.

Intersección de planos cuando sus trazas se cortan fuera de los límites del dibujo.

Las trazas, rectas intersección de los planos dados con los planos de proyección, se cortan fuera de los límites del dibujo de modo que no podemos operar como viene siendo habitual. Para resolver el problema empleamos el método general expuesto al comienzo del tema de intersecciones, tomando como auxiliares planos que no sean los de proyección como hasta ahora sino otros de sencillo trazado, generalmente horizontales o frontales. Pueden darse tres casos generales:

1. Intersección de planos cuando sus trazas verticales se cortan fuera de los límites del dibujo.

Tomamos como plano auxiliar un plano horizontal O, este corta a los dos dados P y Q en las rectas R y S siendo la intersección de ambas entre sí el punto A. Las trazas horizontales de los planos dados se cortan en el punto H. Uniendo los puntos H y A obtenemos la recta intersección buscada I. Fig. 60 En la figura 61, se resuelve el problema en sistema diédrico, las rectas R y S por pertenecer al plano horizontal O, son rectas horizontales de los planos Q y P respectivamente. La recta definida por las proyecciones de los puntos H y A (a’, a y h’, h) es la recta solución.

2. Intersección de planos cuando sus trazas horizontales se cortan fuera de los límites del dibujo.

El ejercicio se resuelve en la figura 62 de igual modo que en el ejercicio precedente. Tomamos como plano auxiliar en este caso un plano frontal.

3. Intersección de planos cuando sus trazas horizontales y verticales se cortan fuera de los límites del dibujo.

En este caso tomamos dos planos auxiliares que en el ejercicio de la figura 63 son frontales, estos generan con los planos dados P y Q dos rectas intersección cada uno, el plano O genera con los planos Q y P las rectas frontales R y S que se cortan en el punto A. El plano W genera con los planos Q y P dados las rectas frontales F y T que se cortan en el punto B. Uniendo las proyecciones diédricas homónimas de los puntos A y B obtenemos las proyecciones i’ e i de la recta I intersección de P y Q buscada. Fig 63.

INTERSECCIÓN RECTA PLANO

Intersección de una recta con un plano oblicuo.

La intersección de una recta R y un plano Q es un punto A. Para saber dónde está situado este punto A, hacemos pasar por R, un plano cualquiera P auxiliar, generalmente proyectante y calculamos la intersección S de éste con el plano dado. El punto de corte de las rectas S obtenida y R dada, será el punto buscado. Fig. 64. Por ser el plano auxiliar tomado proyectante horizontal, las proyecciones horizontales de las rectas R dada, S intersección de los planos Q dado y auxiliar y el punto de intersección I, están contenidas en su traza horizontal P. Fig. 65

Intersección recta con plano que pasa por LT.

Dado el plano Q definido por el punto A en él contenido, para determinar su intersección con la recta R, trazamos un plano auxiliar F frontal que pase por A y uno proyectante horizontal P que contenga a R. El plano frontal F se corta con el plano Q dado generando la recta G frontal y con el plano P auxiliar la recta T vertical, ambas rectas pertenecen al plano frontal F y se cortan en el punto B. Uniendo el punto B hallado con el punto O perteneciente a los planos Q y P obtenemos la recta S perteneciente al plano P auxiliar y a Q dado. La recta S hallada, intersección de los planos Q y P y la recta R dada son coplanarias, ambas pertenecen al plano auxiliar P y se cortan en el punto X, punto de intersección buscado entre la recta R y el plano Q. Fig. 66.

El método para calcular puntos de intersección entre una recta y un plano consiste, como hemos visto, en hacer pasar por la recta un plano auxiliar que genere una intersección (recta) rápida sobre el plano dado, el punto de corte entre la intersección obtenida y la recta dada es el punto de intersección de la recta y el plano. Este ejercicio se resuelve de idéntico modo que el ejercicio anterior, siendo P el plano auxiliar y S la recta intersección obtenida. Su trazado se complica pues el plano dado pasa por la línea de tierra teniendo por tanto sus trazas coincidentes con esta, es por esto por lo que y para calcular la recta intersección S entre P y Q, tenemos que tomar el plano auxiliar frontal F y un punto O de la línea de tierra perteneciente a P. (Véase intersección de un plano con el primer bisector en este mismo tema).

INTERSECCIÓN DE TRES PLANOS.

La intersección de tres planos es un punto cuando los planos no son paralelos entre sí, un ejemplo lo es el propio ángulo triedro (ángulo formado por tres planos) formado entre los planos vertical, horizontal y de perfil del sistema diédrico, se generan tres rectas de intersección que concurren en un mismo punto, vértice del ángulo. Para calcular el punto de intersección de tres planos dados calculamos la recta intersección entre dos de ellos y seguidamente el punto de intersección de la recta así obtenida con el tercer plano. En el ejercicio de la figura 67, se calcula la intersección de tres planos dados P oblicuo, T paralelo a la línea de tierra y Q proyectante vertical. Para ello calculamos la recta R intersección entre los planos P y T. Auxiliándonos de un cuarto plano proyectante horizontal O, que contiene a R y genera la recta intersección S sobre Q, calculamos el punto de intersección A entre R y Q.

AMPLIACIÓN

SISTEMA DIÉDRICO

 

        SISTEMA DIÉDRICO

INTRODUCCIÓN

Forma parte de los llamados Sistemas de Representación Gráfica (Sistemas Axonométrico, Acotado, Cónico, etc…) estudiados en Geometría Descriptiva, esta tiene por objeto la representación en el plano de elementos o superficies tridimensionales distribuidos en el espacio.

Surge de la necesidad de sistematizar la estereometría  (corte y mesura) de las piedras empleadas en las construcciones de la época y es en el siglo XVIII cuando Gaspar Monge, geómetra, físico y matemático francés (nacido en 1746 en Francia y considerado como el verdadero padre de la Geometría Descriptiva), sistematiza y hace gráficas las transformaciones y procesos estudiados hasta entonces por medios exclusivamente matemáticos, por lo que también se le denomina Sistema de Monge.

SIGNIFICADO

Se denomina Sistema por pertenecer a los Sistemas de Representación Gráfica (Diédrico, cónico, axonométrico…) .

Se denomina Diédrico, por utilizar, como sistema de referencia un ángulo Diédro o ángulo comprendido entre dos planos (di= dos, edro= plano), en este caso recto.

Se denomina Ortogonal por emplear proyecciones Cilíndricas Ortogonales para la representación de los diversos elementos distribuidos en el espacio.

ELEMENTOS DEL SISTEMA DIÉDRICO ORTOGONAL 

Los planos de proyección (diedro ortogonal) y referencia se denominan en SDO, PLANO VERTICAL (PV) y PLANO HORIZONTAL (PH), en ellos se proyectan ortogonalmente las proyecciones verticales y horizontales respectivamente, de los elementos a representar.

La recta intersección de ambos planos se denomina LÍNEA DE TIERRA (LT).

Los espacios o regiones comprendidos entre los planos horizontal y vertical, se denominan DIEDROS, son cuatro en total, designándose como se indica en la ilustración. Además de estos elementos, principales, se utilizan con frecuencia otros como son:

PLANO DE PERFIL (PP), que es un plano perpendicular al vertical y horizontal, se utiliza cuando con las proyecciones horizontal y vertical no obtenemos suficientes datos del elemento representado y necesitamos por tanto otra proyección más, la de perfil en este plano.

PLANOS BISECTORES, son planos que dividen en dos ángulos iguales a los Diedros, son dos los bisectores. El espacio formado entre estos y los planos de proyección horizontal y vertical se denomina OCTANTE, son ocho los octantes, de ahí su nombre, se designan del 1º al 8º tal y como se indica en la ilustración de la figura 6.

SISTEMA DIÉDRICO. PUNTO: REPRESENTACIÓN, COORDENADAS Y ALFABETO DEL PUNTO.

Representación de un punto.

Un punto “A” se representa en este sistema mediante sus proyecciones ortogonales sobre el plano vertical y el horizontal. Estas proyecciones se denominan vertical y horizontal y se designan, con minúscula prima o mayúscula y subíndice 2 (a’ · A2) y minúscula o mayúscula y subíndice 1 (a · A1) respectivamente. Fig.7

Cuando trabajamos en Sistema Diédrico, hacemos coincidir el Plano Vertical de proyección del sistema de referencia con el papel del dibujo, representamos la línea de tierra quedando, de este modo, encima o debajo de ella las proyecciones efectuadas en este plano.

Lo proyectado sobre el Plano Horizontal queda sin embargo escorzado en la propia Línea de Tierra por lo que no es representativo. Para evitar esta situación abatimos dicho plano 90º en el sentido de las agujas del reloj, empleando como charnela o “bisagra” la propia Línea de Tierra, hasta hacerlo coincidir con el vertical de proyección. De este modo tenemos sobre el papel también las proyecciones horizontales de los elementos y ambos planos, Horizontal y Vertical, superpuestos sobre el papel del dibujo. Fig.8

El punto queda así representado por sus proyecciones horizontal y vertical entorno a la Línea de Tierra, sobre una perpendicular a esta trazada (en línea de puntos) y a unas distancias determinadas: la distancia de la proyección vertical a LT denominada COTA y la distancia de la proyección horizontal a LT denominada ALEJAMIENTO. Fig.9

La Cota es positiva cuando la proyección vertical del punto está por encima de LT, negativa si está por debajo y nula si está en ella.

El Alejamiento se considera positivo si la proyección horizontal está debajo de LT, negativo si está por encima y nulo cuando coincide con LT.

Coordenadas de un punto.

Un punto A, puede venir dado por sus COORDENADAS A (x, y, z), en donde “x” es la distancia sobre la línea de tierra desde la intersección de la perpendicular que contiene las proyecciones del punto con la propia línea de tierra hasta donde situemos el origen de coordenadas, “y” es el alejamiento y “z” la cota.

EJEMPLO: Para un origen de coordenadas situado en el extremo izquierdo de la línea de tierra, representamos el punto A (3, 2, 1).

El eje X es positivo del origen de coordenadas hacia la derecha y negativo en caso contrario. Fig.10

Alfabeto del punto.

Según la ubicación de un punto respecto del sistema de referencia establecido, así serán su cota y alejamiento y por tanto su representación en S.D.O. Un punto puede estar situado:

 -En uno de los cuatro Diedros, (si está en el primero tendrá cota y alejamiento positivos, negativos ambos en el 3º, positiva la cota y negativo el alejamiento en el 2º y viceversa en el 4º.)

 -Contenido en los Planos de Proyección, en cuyo caso tendrá nula la cota si está en el PH o el alejamiento si está en PV.

 -Contenido en un plano bisector (tendrán igual magnitud su cota y su alejamiento, positivos ambos en el 1º diedro, negativos ambos en el 3º diedro y uno positivo y otro negativo en los diedros 2º y 4º).

 -En la Línea de Tierra. En este caso son nulos los valores para la cota y el alejamiento.

RECTA. REPRESENTACIÓN, TRAZAS Y TIPOS DE RECTAS.

Representación de la recta en SDO

Sabemos que una recta es una sucesión de puntos y que dos puntos determinan una recta. En SDO una recta se representa mediante sus proyecciones sobre el Plano Vertical y el Plano Horizontal, denominadas Proyección Vertical y Proyección Horizontal de la recta respectivamente y designadas por minúscula prima y minúscula respectivamente (r’, r). Según algunos autores por minúscula con subíndices 2 y 1 respectivamente (r2, r1).

Para poder representar dichas proyecciones, bastará con representar las proyecciones de dos de los puntos de la recta y unir las proyecciones homólogas. Por ejemplo, para representar la recta R, representamos primero las proyecciones verticales y horizontales de A y B, puntos contenidos en ella. Uniendo -a’- con -b’- tendremos la proyección vertical de R, r’. Uniendo -a- con -b-, la proyección horizontal de “R”, r. Fig.12.

Pertenencia de un punto a una recta.

Un punto pertenece a una recta cuando las proyecciones vertical y horizontal del punto pertenecen a las proyecciones vertical y horizontal de la recta respectivamente.

Ejemplo.:

El punto C pertenece a R pues c’ y c pertenecen a r’ y r respectivamente. Los puntos D,E y F no pertenecen a R pues alguna de sus proyecciones o ambas no pertenecen a R. Fig.13.

El punto G no pertenece a R pues las proyecciones que coinciden con r’ y r no son las homólogas sino las contrarias, g está sobre r’ y g’ está sobre r, están invertidas y por tanto la pertenencia es solo aparente. Fig.14

Trazas de la recta

Se denominan Trazas de la recta a los puntos de intersección de esta con los planos de proyección horizontal, vertical y, en su caso, de perfil. Como cualquier otro punto, las trazas de la recta se representan por sus proyecciones horizontales y verticales.

Se denomina Traza Horizontal de una recta a la intersección de la recta con el plano horizontal de proyección, se designa con hache mayúscula, H y como cualquier otro punto, tiene proyección vertical (h’) y proyección horizontal (h), esta última coincidente con la verdadera traza. Fig.15.

Se denomina Traza Vertical de una recta a la intersección de la recta con el plano vertical de proyección, se designa con uve mayúscula, V y como cualquier otro punto tiene proyección vertical (v’) coincidente con la verdadera traza y proyección horizontal (v). Fig.15.

Tipos de rectas

Paralelas a alguno de los planos de proyección o a ambos:

Recta horizontal. La que es paralela al plano de proyección horizontal. Su proyección vertical es paralela a LT. Fig.17

Recta frontal. La que es paralela al plano de proyección vertical. Su proyección horizontal es paralela a LT. Fig.18

Recta paralela a la línea de tierra. Sus proyecciones son paralelas a LT. Fig. 19

Perpendiculares a alguno de los planos de proyección:

Recta vertical. Perpendicular al plano horizontal de proyección. Su proyección vertical es perpendicular a LT. y su proyección horizontal queda representada por un punto. Fig.20

Recta de punta. Perpendicular al plano vertical de proyección. Su proyección horizontal es perpendicular a LT. y su proyección vertical queda representada por un punto. Fig.21

Recta de perfil. Presenta sus proyecciones normales a LT por pertenecer a un plano de perfil. Ver plano de perfil en este mismo tema. Fig 22.

Recta contenida en un bisector. Sus proyecciones forman un mismo ángulo con LT. En la figura 23 se representa una contenida en el primer bisector, primer diédro.

EL PLANO. REPRESENTACIÓN Y DESIGNACIÓN DE UN PLANO EN S.D.O. TRAZAS.

El plano se representa en S.D.O. por sus TRAZAS. Se denominan Trazas del plano a las rectas intersección de este con los planos vertical y horizontal de proyección.

La Traza Horizontal del plano es la recta intersección de este con el Plano Horizontal de proyección y la Traza Vertical es la intersección del plano con la el Plano Vertical de proyección. Si el plano es oblicuo, proyectante o de perfil, dichas trazas coinciden en un punto sobre la Línea de Tierra.

El plano en el espacio se designa con letra mayúscula, Q, con mayúscula prima la Traza Vertical, Q’ y mayúscula la Traza Horizontal, Q. Según algunos autores la designación correcta debe ser a1, a2 o cualquier otra letra griega acompañada de los subíndices 1 y 2 para las trazas horizontal y vertical respectivamente. Fig.25

DETERMINACIÓN DE UN PLANO.

Un plano puede venir dado directamente en sistema diédrico si nos aclaran la situación exacta de sus trazas. Frecuentemente tendremos que hallar las trazas de un plano que venga determinado de otro modo. Un plano puede venir determinado (cuatro casos).:

1. Determinación de un plano por dos rectas que se cortan, R y S.

Por una recta pueden pasar infinitos planos pero por dos rectas que se cortan solo pasa un plano. Fig. 28

Dadas las rectas R y S que se cortan en un punto A si queremos trazar un plano Q que contenga a R, debemos hacer pasar las trazas de este por las de la recta, son infinitos los planos que se pueden trazar que contengan a la recta.

Si queremos que, además de contener a R, el plano trazado Q contenga a S, haremos pasar las trazas de Q no solo por las de R sino también por las de S, de esta forma obtenemos el único plano determinado por R y S que se cortan. Fig. 29A y B.

2. Determinación de un plano por un punto y una recta, B y T.

Si trazamos desde el punto B una recta L que se corte con la dada T en un punto cualquiera P, estamos en la misma situación del ejercicio anterior, tenemos dos rectas L y T que se cortan, calculamos sus trazas y hacemos pasar por las homologas las trazas del plano buscado N. Fig.30.

3. Determinación de un plano por tres puntos no alineados, C, D y E.

Uniendo los puntos dos a dos (el C con el D y el E con el D, por ejemplo), mediante las rectas X y W, nos situamos de nuevo en el primer caso, siendo D en este caso el punto donde se cortan. Fig.31.

4. Determinación de un plano por dos rectas paralelas entre sí, M y Ñ.

Por dos rectas paralelas pasa un solo plano.

En SDO, dos rectas paralelas mantienen sus proyecciones homólogas también paralelas. Uniendo las trazas homólogas de estas tendremos definido el plano que determinan o en el que están contenidas, O. Fig.32.

TIPOS DE PLANOS.

En base a la posición de los planos dibujados respecto del sistema de referencia, se pueden tipificar los siguientes grupos y subgrupos:

1. Planos oblicuos a los planos de proyección

Los que no son paralelos ni perpendiculares a los planos de referencia del sistema. Presentan sus trazas oblicuas respecto de la línea de tierra. Fig.33.

2. Planos perpendiculares a los planos de proyección

Son perpendiculares a alguno de los planos de proyección o a ambos, se utilizan frecuentemente como planos auxiliares. Hay tres tipos:

Plano proyectante horizontal.

Es perpendicular al plano horizontal de proyección. Su traza vertical es perpendicular a la línea de tierra. Se denomina Proyectante Horizontal pues las proyecciones horizontales de todos los elementos contenidos en él coinciden en la traza horizontal de dicho plano. Fig.34

Plano proyectante vertical.

Es perpendicular al plano vertical de proyección. Su traza horizontal es perpendicular a la línea de tierra. Se denomina Proyectante Vertical pues las proyecciones verticales de todos los elementos contenidos en él coinciden en la traza vertical de dicho plano. Fig.35

Plano de perfil.

Son perpendiculares al plano vertical y horizontal de proyección. Sus trazas se presentan normales a la línea de tierra. Las proyecciones de los elementos en ellos contenidos, coinciden con sus trazas por lo que, y con objeto de obtener una proyección más representativa de sus elementos, abatimos este plano sobre el vertical de proyección presentándose de este modo en verdadera magnitud y forma. En la figura 40, abatimos un plano de perfil y apreciamos de este modo la ubicación de los puntos A y B en él contenidos. Fig.36

3. Planos paralelos a los planos de proyección.

Son paralelos a alguno de los planos de proyección, hay dos tipos:

Plano Horizontal.

Paralelo al horizontal de proyección. Su traza vertical es paralela a la línea de tierra y contiene las proyecciones verticales de los elementos contenidos en él. Por ser paralelo al plano horizontal no tiene traza horizontal. Fig. 37.

Plano Frontal.

Paralelo al vertical de proyección. Su traza horizontal es paralela a la línea de tierra y contiene las proyecciones horizontales de los elementos contenidos en él. Por ser paralelo al plano vertical no tiene traza vertical. Fig. 38.

4. Paralelos a la línea de tierra.

Presentan sus trazas vertical y horizontal paralelas a la línea de tierra. En la figura se traza un punto A perteneciente al plano, auxiliándonos de una recta R del plano. Fig. 39.

5. Planos que pasan por LT

Su intersección con los planos de referencia es la propia línea de tierra por lo que sus trazas no son representativas. Para representarlos se trazan las proyecciones de uno de sus puntos y se dibujan dos trazos por debajo de la línea de tierra, entorno a la recta de perfil que pasa por dicho punto. En la figura, se ha abatido la recta de perfil antedicha obteniéndose de este modo una idea clara de la ubicación relativa del plano. Obsérvese que esta recta es normal y corta a LT. Fig. 40.

6. Planos perpendiculares a los planos bisectores.

Plano perpendicular al primer bisector.

Calculamos la traza de perfil del plano bisector (coincidente con r”) y le trazamos una perpendicular en cualquiera de sus puntos (a”), quedando así determinada la traza de perfil Q” del plano buscado. Deshacemos el abatimiento del plano de perfil P y obtenemos Q y Q’. R es la recta intersección del bisector y el plano Q trazado, contiene al punto A equidistante a los planos de proyección y a X punto perteneciente a LT.

Son infinitos los planos normales al primer bisector, la única condición es que muestren sus trazas sobre un tercer plano de perfil, normales entre sí, las trazas vertical y horizontal del plano trazado, forman en cualquier caso idénticos ángulos con la línea de tierra. El trazado Q pasa además por X y A. Fig. 41. Un caso particular de plano normal a los bisectores es el plano de perfil, perpendicular a ambos bisectores y a los propios de proyección. 

Plano perpendicular al segundo bisector.

Los ángulos que forman sus trazas con LT son idénticos pero en sentido contrario.

RECTAS PARTICULARES DEL PLANO.

Rectas horizontales del plano.

Son rectas horizontales y pertenecientes al plano. Fig 42

Son rectas frontales y pertenecientes al plano. Fig 43

Rectas de máxima pendiente e inclinación del plano.

Definen la dirección de máxima pendiente o inclinación de un plano, según se mida con el plano horizontal o vertical de proyección respectivamente.

Recta de máxima pendiente.

Es la dirección R por donde discurriría una gota de agua en un plano cualquiera Q, si hiciéramos coincidir el plano horizontal de proyección con el suelo. Será por tanto la recta del plano que forme mayor ángulo con el plano horizontal de proyección. En S.D.O. muestra esta recta R su proyección horizontal, r, perpendicular a la traza horizontal del plano. Naturalmente, esta recta está contenida en el plano Q, y por tanto sus trazas coincidentes con las homólogas de dicho plano. Fig.44

Es la dirección T por donde discurriría una gota de agua en un plano cualquiera P, si hiciéramos coincidir el plano vertical de proyección con el suelo. En S.D.O. muestra esta recta T su proyección vertical, t’, perpendicular a la traza vertical del plano. Naturalmente, esta recta está contenida en el plano P y por tanto sus trazas coincidentes con las homólogas de dicho plano. Fig. 45.

Rectas de perfil de un plano.

Las trazas de una recta de perfil R contenida en un plano Q coinciden con las trazas del plano, para conocer la ubicación de la recta con relación a los planos de referencia, abatimos en el plano vertical su proyección sobre un plano de perfil auxiliar P. Fig 46.

RESUMEN