TRANSFORMACIONES GEOMÉTRICAS EN EL PLANO
lunes, 6 de diciembre de 2021
domingo, 21 de noviembre de 2021
GEOMETRÍA CONCEPTOS
¿QUÉ ES LA GEOMETRÍA?
La geometría es una rama de las matemáticas que se ocupa del estudio de las propiedades de las figuras en el plano o el espacio, incluyendo: puntos, rectas, planos. Es la base teórica de la geometría descriptiva o del dibujo técnico.
LA GEOMETRÍA DESCRIPTIVA ESTUDIA
lunes, 6 de septiembre de 2021
Curso 2021-22 .INTRODUCCIÓN DIBUJO TÉCNICO
DIBUJO TÉCNICO INTRODUCCIÓN
Para hablar de dibujo técnico primero hay que definir que un dibujo es una figura, imagen o delineación que se suele hacer manualmente con ayuda de alguna herramienta (un lápiz, un pincel) sobre distintos materiales. El concepto de técnico, por otra parte, hace referencia a un procedimiento vinculado a la ciencia cuyo objetivo es la obtención de un cierto resultado.
El dibujo técnico también se ha definido como el sistema de representación gráfica de objetos ya existentes o bien de prototipos, atendiendo a normas y convenciones preestablecidas por instituciones reguladoras. Eso permite describir de forma precisa y con claridad las dimensiones, formas y características de esos objetos materiales.
Actualmente el dibujo técnico puede desarrollarse con ayuda de la informática. Existen ciertos softwares que permiten realizar proyecciones y cálculos que facilitan el dibujo, esta herramienta se conoce como CAD (Diseño Asistido por Computadora). En cuanto a los instrumentos manuales, los más usuales son las reglas, las escuadras y los compases.
-El dibujo técnico posee 3 características que deben ser respetadas a la hora de realizar un trabajo:
• Grafico.
• Universal.
• Preciso.
Diferencias entre el dibujo técnico y dibujo artístico
El dibujo técnico es objetivo, sólo transmite información precisa sin preocuparse por transmitir una emoción. En cambio, el dibujo artístico puede ser subjetivo, transmite emociones y causa una impresión en los espectadores.
Tipos de dibujo técnico según su uso:
• Dibujo Técnico Arquitectónico:
El dibujo arquitectónico abarca una gama de representaciones gráficas con las cuales realizamos los planos para la construcción de edificios, casas, autopistas, iglesias, fábricas y puentes entre otros. Se dibuja el proyecto con instrumentos precisos, con sus respectivos detalles, ajuste y correcciones, donde aparecen los planos de planta, fachadas, secciones, perspectivas, columnas, detalles entre otros.
• Dibujo Mecánico:
El dibujo mecánico se emplea en la representación de piezas o partes de máquinas, maquinarias, vehículos como grúas, motos, aviones, helicópteros y máquinas industriales. Los planos que representan un mecanismo simple o una máquina formada por un conjunto de piezas son llamados planos de conjunto; y los que representa un sólo elemento, plano de pieza. Los que representan un conjunto de piezas con las indicaciones gráficas para su colocación, y armar un todo, son llamados planos de montaje.
• Dibujo Eléctrico:
Este tipo de dibujo se refiere a la representación gráfica de instalaciones eléctricas en una industria, oficina o vivienda o en cualquier estructura arquitectónica que requiera de electricidad. Mediante la simbología correspondiente se representan acometidas, tablero principal, línea de circuitos, interruptores, toma corrientes, salidas de lámparas entre otros.
• Dibujo Electrónico:
Es aquel que expresa simbólicamente conexiones y diseño de componentes electrónicos como pueden ser resistencias, inductores, transistores, fuentes de alimentación, etc. Se pueden utilizar en equipos de comunicaciones, militar, científico, de investigación o de control industrial.
• Dibujo Geológico:
El dibujo geológico se emplea en geografía y en geología, en él se representan las diversas capas de la tierra empleando una simbología y da a conocer los minerales contenidos en cada capa. Se usa mucho en minería y en exploraciones de yacimientos petrolíferos.
• Dibujo Topográfico:
El dibujo topográfico nos representa gráficamente las características de una determinada extensión de terreno, mediante signos convencionalmente establecidos. Nos muestra los accidentes naturales y artificiales, cotas o medidas, curvas horizontales o curvas de nivel.
• Dibujo Urbanístico:
Este tipo de dibujo se emplea en la organización de ciudades: en la ubicación de centros urbanos, zonas industriales, calles, avenidas, jardines, autopistas, zonas recreativas entre otros. Se dibujan anteproyectos, proyectos, planos de conjunto, planos de pormenor.
jueves, 13 de mayo de 2021
PERSPECTIVA CÓNICA OBLICUA.EJERCICIOS
PERSPECTIVA CÓNICA OBLICUA
Perspectiva Cónica Oblicua. Hablamos de perspectiva cónica oblicua cuando ninguna de las caras del objeto es paralela al plano del cuadro y, por tanto, tiene sus caras en direcciones oblicuas respecto al observador.
En primer lugar vamos a ver un vídeo sencillo a modo de introducción.
En este vídeo se explica más en profundidad de la perspectiva cónica oblicua
Método de los puntos métricos para dibujar una pieza en perspectiva cónica
CÓNICA FRONTAL EJERCICIOS BÁSICOS
PERSPECTIVA CÓNICA FRONTAL EJERCICIOS BÁSICOS
Hablamos de perspectiva cónica frontal cuando una de las caras del objeto es paralela al plano del cuadro y al observador, es decir, cuando una de las caras es frontal a nuestra vista. En este caso, sólo habrá un punto de fuga que coincide con el punto principal (P)
EL PUNTO
En la Perspectiva Cónica Frontal, el único Punto de Fuga será el punto P.
Cualquier recta perpendicular a la Línea de Tierra tiene su Punto de Fuga en P.
Aplicaremos este principio al punto A. Dibujaremos una recta perpendicular a LT por A y el punto de corte 1 con la LT lo uniremos con P.
Por tanto, la recta 1-P es la representación cónica de la recta A-1.
Para encontrar la profundidad a la que se encuentra el punto A utilizaremos los Puntos Métricos D y D’. Dibuja una recta a 45º desde el punto A que corte a la LT en 2. Une el punto 2 con D para encontrar A en la cónica.
Existe una última forma de comprobar que la posición del punto A en la cónica es la correcta. Une el punto A en planta con el punto V y en esta recta debe estar el punto A en perspectiva.
LA ALTURA
Supongamos ahora que por encima del punto A se encuentra un punto B a una altura de 2 cm.
Dibujaremos sobre la Línea de Tierra (que, si recuerdas, es la línea de verdaderas magnitudes) una altura en vertical de 2 cm y la proyectaremos hacia el punto de fuga P. Desde el punto A tendremos que dibujar una recta vertical que nos definirá la posición del punto B en la cónica.
Vamos a observar en estos vídeos un ejercicio básico .¿Cómo dibujar un cubo en cónica frontal?
Ahora en este vídeo vamos observar cómo se realiza un suelo de baldosas.
Ejercicio básico
Vamos a dibujar un suelo mediante una perspectiva cónica frontal cuyos datos son: Distancia entre la LT y LH=70mm P Y V= 80 mm.Cada baldosa mide 2 cm.
PERSPECTIVA CÓNICA
PERSPECTIVA CÓNICA
FUNDAMENTOS
La perspectiva cónica de una figura es la representación de esta sobre un plano, tal y como la vemos en la realidad.
Aunque a lo largo de la historia se han llevado a cabo muchos intentos por representar la realidad sobre el lienzo de forma tridimensional, con toda su profundidad, es en el Renacimiento (S XV) con Paolo Uccello, Piero de la Francesca y Leonardo da Vinci, cuando se aborda el tema con autentico rigor, obteniendo representaciones pictóricas sorprendentes para la época.
Si a través de un cristal (cuadro), miramos un objeto con sólo un ojo (centro de proyección) manteniendo el otro cerrado, y dibujamos sobre el cristal el objeto, tal y como lo vemos, obtenemos la perspectiva cónica o central del mismo.
La perspectiva se divide en dos partes principales: perspectiva lineal o cónica y perspectiva luminar o aérea.
La perspectiva lineal es aquella que comprende el estudio y representación por medio del dibujo, de la forma o contorno de los objetos en un supuesto plano vertical, con precisión matemática. El resultado produce en nuestra vista un resultado real o verdadero, es decir, el objeto se muestra tal y como se ve desde un punto elegido por el observador, con sus deformaciones naturales y reducciones aparentes por defecto de la distancia.
Se denomina luminar o aérea cuando representan la forma corpórea de los objetos mediante claroscuros y sombras, tanto propias como arrojadas.
La perspectiva lineal se divide a su vez en:
-Perspectiva frontal o de un punto.
-Perspectiva oblicua o de dos puntos.
-Perspectiva oblicua o de tres puntos.
ELEMENTOS DE LA PERSPECTIVA CÓNICA
En primer lugar tenemos el plano del cuadro (PC) sobre el que se proyectará el objeto. Podemos decir que el mismo es como un papel transparente, perpendicular al suelo y situado entre el objeto y el observador.
El punto de vista (V) es el observador que mira el objeto. Su posición (si mira desde arriba, desde cerca o desde la izquierda, etc.) determina la forma de proyectarse el objeto en el plano del cuadro.
La línea de horizonte (LH) es una línea horizontal respecto al suelo, sobre la que se situarán el punto o los puntos de fuga. Esta línea imaginaria se encuentra a la altura de los ojos del observador.
El punto principal (P) se sitúa en la línea de horizonte. En este punto convergerán o fugarán todas las líneas paralelas a una dirección. Dependiendo del número de puntos de fuga será el tipo de perspectiva cónica.
Por último, la línea de tierra (LT) es otra línea imaginaria resultado de la intersección del plano del cuadro con el plano del suelo. Ambos planos son perpendiculares entre sí.
La importancia de la situación del observador respecto a la pieza
En el dibujo que ves en pantalla observarás cómo resultan las proyecciones del cubo sobre el plano del cuadro en perspectiva cónica. El dibujo es justo lo que vería el espectador desde la posición en la que mira el cubo.
Observa cómo aparecen los elementos que hemos definido anteriormente (LH, P, V y LT), así como la posición del cubo visto por el observador. El punto de vista (V) aparece abatido sobre el plano del cuadro (PC), para determinar la distancia desde la que mira el observador.
Igualmente, si cambiamos la altura desde la que mira el observador, la visión perspectiva de la pieza se verá de otra forma.
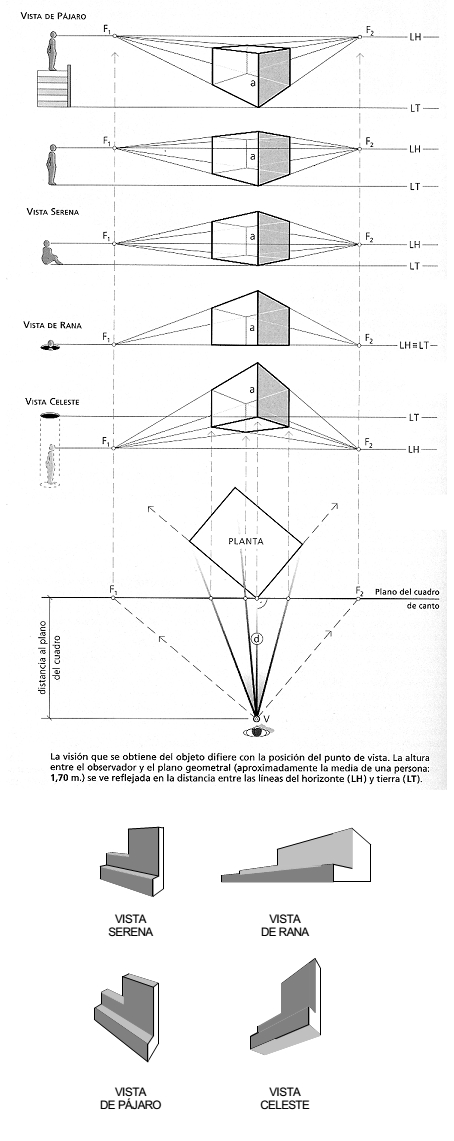
En este enlace puedes observar los diferentes puntos de vista
http://recursostic.educacion.es/artes/plastic/web/cms/index.php?id=3933
PERSPECTIVA CÓNICA FRONTAL
PERSPECTIVA CÓNICA CON DOS PUNTOS DE FUGA
PERSPECTIVA TRES PUNTOS DE FUGA
lunes, 12 de abril de 2021
REPRESENTACIÓN NORMALIZADA
NORMALIZACIÓN
La Normalización es una actividad colectiva orientada a establecer solución a problemas repetitivos.
Los objetivos de la normalización, pueden concretarse en tres:
-La economía, ya que a través de la simplificación se reducen costos.
-La utilidad, al permitir la intercambiabilidad.
-La calidad, ya que permite garantizar la constitución y características de un determinado producto.
NORMAS ISO
Ante la aparición de todos estos organismos nacionales de normalización, surgió la necesidad de coordinar los trabajos y experiencias de todos ellos, con este objetivo se fundó en Londres en 1926 la:
Internacional Federación of the National Standardization Associations – ISA
Normas UNE españolas
A partir de 1986 las actividades de normalización y certificación N+C, recaen en España en la entidad privada AENOR (Asociación Española de Normalización). AENOR es miembro de los diferentes organismos internacionales de normalización:
Formatos normalizados
Líneas normalizadas
Clases de líneas
En los dibujos técnicos se utilizan diferentes tipos de líneas, sus tipos y espesores, han sido normalizados en las diferentes normas. En esta página no atendremos a la norma UNE 1-032-82, equivalente a la ISO 128-82.
Espaciado entre las líneas
El espaciado mínimo entre líneas paralelas (comprendida la representación de los rayados) no debe nunca ser inferior a dos veces la anchura de la línea más gruesa. Se recomienda que este espacio no sea nunca inferior a 0,7 mm.
Orden de prioridad de las líneas coincidentes
En la representación de un dibujo, puede suceder que se superpongan diferentes tipos de líneas, por ello la norma ha establecido un orden de preferencias a la hora de representarlas, dicho orden es el siguiente:
1.Contornos y aristas vistos.
2.Contornos y aristas ocultos.
3.Trazas de planos de corte.
4.Ejes de revolución y trazas de plano de simetría.
5.Los contornos contiguos de piezas ensambladas o unidas deben coincidir, excepto en el caso de secciones delgadas negras.
5.Los contornos contiguos de piezas ensambladas o unidas deben coincidir, excepto en el caso de secciones delgadas negras.
Terminación de las líneas de referencia
Una línea de referencia sirve para indicar un elemento (línea de cota, objeto, contorno, etc.).
Las líneas de referencia deben terminar:
-En un punto, si acaban en el interior del contorno del objeto representado.
-En una flecha, si acaban en el contorno del objeto representado.
-Sin punto ni flecha, si acaban en una línea de cota.
-Líneas de centros de gravedad.
-Líneas de proyección.
Orientaciones sobre la utilización de las líneas normalizadas
1,Las líneas de ejes de simetría, tienen que sobresalir ligeramente del contorno de la pieza y también las de centro de circunferencias, pero no deben continuar de una vista a otra.
2.En las circunferencias, los ejes se han de cortar, y no cruzarse, si las circunferencias son muy pequeñas se dibujarán líneas continuas finas.
3.El eje de simetría puede omitirse en piezas cuya simetría se perciba con toda claridad.
4.Los ejes de simetría, cuando representemos media vista o un cuarto, llevarán en sus extremos, dos pequeños trazos paralelos.
5.Cuando dos líneas de trazos sean paralelas y estén muy próximas, los trazos de dibujarán alternados.
6.Las líneas de trazos, tanto si acaban en una línea continua o de trazos, acabarán en trazo.
7.Una línea de trazos, no cortará, al cruzarse, a una línea continua ni a otra de trazos.
8.Los arcos de trazos acabarán en los puntos de tangencia.
Introducción de las tres vistas básicas
En primer lugar vamos a aprender cómo se sitúan las vistas diédricas sobre el cubo isométrico ,para dibujar una pieza en tres dimensiones.
En perspectiva caballera
En este vídeo se explica la diferencia entre el sitema europeo ( primer diedro) y el sistema americano ( tercer diedro).Nosotros trabajamos en sistema europeo ,pero hay que conocer la disposición en el otro sistema.
EL CROQUIS
El croquis es una representación rápida realizada a mano alzada, sin instrumentos de dibujo y con medidas aproximadas, que nos permiten la visualización e interpretación de una pieza determinada. Que sea a mano alzada, no quiere decir que haya que hacerlo sin seguir unas normas .
Las vistas deben estar bien situadas ,según el sistema europeo , y coincidir unas bajo las otras .Aunque las medidas son a mano alzada deben ser aproximadas a la solución real .
Ejemplos de croquis
Las vistas deben estar bien situadas ,según el sistema europeo , y coincidir unas bajo las otras .Aunque las medidas son a mano alzada deben ser aproximadas a la solución real .
Ejemplos de croquis
miércoles, 7 de abril de 2021
ACOTACION
ACOTACIÓN
La acotación es el proceso de anotar, mediante líneas, cifras, signos y símbolos, las medidas de un objeto, sobre un dibujo previo del mismo, siguiendo una serie de reglas y convencionalismos, establecidos mediante normas.
Os envié por papas un resumen de las normas básicas
Os envié por papas un resumen de las normas básicas
Observar los principios básicos en estos vídeos.
Leer esta presentación
https://issuu.com/dibujoisamarbue/docs/principios_generales_de_acotacion
En estos enlaces vamos a practicar un poco de acotación. Realiza los test de acotación que se indican en estos enlaces.
test_normas_de_acotacion.html#!
CORTES Y SECCIONES
CORTES Y SECCIONES
Introducción
Nos podemos encontrar con piezas complicadas que tienen unas zonas interiores difíciles de representar. Para poder representar estas piezas, aparecen los cortes y las secciones.
Los cortes y secciones se realizan para conseguir mayor claridad en la representación de las piezas que tienen zonas ocultas.
En estos enlaces podéis descargar la teoría de cortes y secciones desarrollada
https://laverdaderamagnitud.files.wordpress.com/2012/05/4cortes.pdf
En estos enlaces podéis descargar la teoría de cortes y secciones desarrollada
https://laverdaderamagnitud.files.wordpress.com/2012/05/4cortes.pdf
Aquí vamos a ver cómo se realizaría un examen de la Paeg con un corte
Este es el enunciado
El vídeo con la solución.
ESCALAS
ESCALAS
La representación de objetos a su tamaño natural no es posible cuando éstos son muy grandes o cuando son muy pequeños.
Esta problemática la resuelve la ESCALA, aplicando la ampliación o reducción necesarias en cada caso para que los objetos queden claramente representados en el plano del dibujo.
Se define la ESCALA como la relación entre la dimensión dibujada respecto de su dimensión real, esto es:
Escala
Si el numerador de esta fracción es mayor que el denominador, se trata de una escala de ampliación, y será de reducción en caso contrario.
La escala 1:1 corresponde a un objeto dibujado a su tamaño real (escala natural).
2:1 ESCALA DE AMPLIACIÓN
1:2 ESCALA DE REDUCCIÓN
1.1 ESCALA NATURAL
Escalas normalizadas
Aunque, en teoría, sea posible aplicar cualquier valor de escala, en la práctica se recomienda el uso de ciertos valores normalizados con objeto de facilitar la lectura de dimensiones mediante el uso de reglas o escalímetros.
Estos valores son:
No obstante, en casos especiales (particularmente en construcción) se emplean ciertas escalas intermedias tales como:
1:25, 1:30, 1:40, etc…
Ejemplos prácticos
EJEMPLO 1
Se desea representar en un formato A3 la planta de un edificio de 60 x 30 metros.
La escala más conveniente para este caso sería 1:200 que proporcionaría unas dimensiones de 30 x 15 cm, muy adecuadas al tamaño del formato.
EJEMPLO 2:
Se desea representar en un formato A4 una pieza de reloj de dimensiones 2 x 1 mm.
La escala adecuada sería 10:1
Escala gráfica
Basado en el Teorema de Thales se utiliza un sencillo método gráfico para aplicar una escala.
Véase, por ejemplo, el caso para E 3:5
1.Con origen en un punto O arbitrario se trazan dos rectas r y s formando un ángulo cualquiera.
2.Sobre la recta r se sitúa el denominador de la escala (5 en este caso) y sobre la recta s el numerador (3 en este caso). Los extremos de dichos segmentos son A y B.
3.Cualquier dimensión real situada sobre r será convertida en la del dibujo mediante una simple paralela a AB.
Contraescala
Triángulo universal de escalas
Mediante un triángulo, podemos construir las escalas más sencillas, tanto normalizadas como no. Como vemos en las figuras, lo podremos hacer mediante un triángulo equilátero de 10 cm de lado, o mediante un triángulo rectángulo isósceles, cuyos catetos midas 10 cm.
Escala decimal de transversal
Con este tipo de escala se puede obtener, con mayor exactitud, las medidas de un segmento a escala, ya que en la denominada contraescala, de la parte izquierda, podremos apreciar las décimas y centésimas de unidad.
En la siguiente imagen podemos ver como hemos construido la escala decimal de transversales 1:20, y en ella hemos indicado dos ejemplos de mediciones sobre la misma, 2,77 m y 1,53 m.
Suscribirse a:
Entradas (Atom)
-
PARALELISMO Y PERPENDICULARIDAD 1. DEFINICIÓN DE PARALELISMO Se dice que dos elementos son paralelos cuando mantienen una distancia cons...
-
PERSPECTIVA CÓNICA FRONTAL 27 de mayo de 2020 Hablamos de perspectiva cónica frontal cuando una de las caras del objeto e... -
ABATIMIENTO Habitualmente, las proyecciones en Sistema Diédrico Ortogonal de los planos, rectas y superficies representadas no muestran su...
